Hidden Markov Models

Hidden Markov Models (HMMs) stand as a pinnacle in the realm of probabilistic graphical models. With applications spanning from speech recognition to bioinformatics and beyond, HMMs have become indispensable tools for modeling sequential data. In this comprehensive guide, we delve deep into the intricacies of Hidden Markov Models, unraveling their hidden states and observable outcomes.

Understanding the Basics

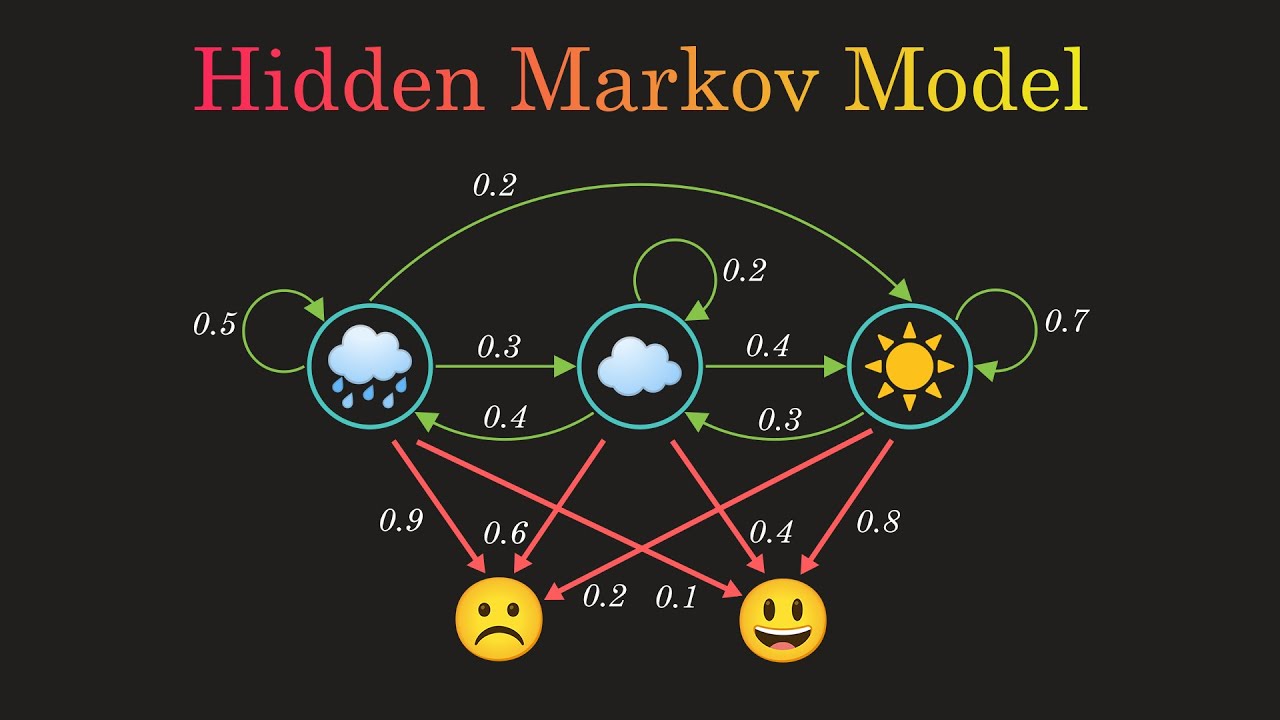
At its core, a Hidden Markov Model is a probabilistic model used to describe sequences of observable events, where each event is associated with a hidden state. The key components of an HMM include:

1. Hidden States (S): These are the unobserved states of the system. They form a Markov chain, meaning the probability of transitioning from one state to another depends only on the current state and not on the sequence of events preceding it.
2. Observations (O): Observable events generated by each hidden state. Each state emits observations according to a probability distribution specific to that state.
3. Transition Probabilities (A): The probabilities of transitioning from one hidden state to another. These are represented by a transition matrix, where each entry (i, j) represents the probability of transitioning from state i to state j.
4. Emission Probabilities (B): The probabilities of emitting each observation from each hidden state. These are represented by an emission matrix, where each entry (i, k) represents the probability of emitting observation k from state i.

Applications of Hidden Markov Models

The versatility of HMMs lends them to a myriad of applications across various domains:

1. Speech Recognition: HMMs are extensively used in speech recognition systems, where they model the relationship between spoken words and their acoustic features. Each word is associated with a sequence of phonemes, and HMMs can efficiently recognize words by decoding the most likely sequence of hidden states given the observed acoustic features.
2. Natural Language Processing (NLP): In NLP tasks such as part-of-speech tagging and named entity recognition, HMMs are employed to model the underlying structure of language sequences. By considering the hidden states as linguistic categories (e.g., noun, verb, adjective), HMMs can accurately label words with their respective parts of speech.
3. Bioinformatics: HMMs find widespread use in biological sequence analysis, particularly in modeling DNA, RNA, and protein sequences. They can identify patterns, such as genes or regulatory elements, within sequences by learning the probabilities of observing different nucleotides or amino acids at each position.
4. Finance: HMMs are applied in financial modeling for tasks such as time series analysis and stock price prediction. By modeling the underlying states of the market (e.g., bull, bear, stagnant), HMMs can help investors make informed decisions based on the observed market data.

Training Hidden Markov Models

Training an HMM involves learning the parameters (transition and emission probabilities) from a given dataset. The most common approach for training HMMs is the Expectation-Maximization (EM) algorithm, specifically the Baum-Welch algorithm. The algorithm iteratively estimates the parameters that maximize the likelihood of the observed data, considering both the observed sequences and the corresponding hidden states.

Challenges and Extensions

While HMMs offer powerful modeling capabilities, they also come with their own set of challenges:

1. Model Complexity: The performance of an HMM heavily depends on the choice of the number of hidden states and the structure of the model. Selecting an optimal model structure often involves trade-offs between model complexity and generalization.
2. Overfitting: Like many machine learning models, HMMs are susceptible to overfitting, especially when the training data is limited. Regularization techniques and model selection criteria, such as the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC), can help mitigate overfitting.
3. Non-stationary Data: HMMs assume that the underlying system is stationary, meaning the transition probabilities between hidden states remain constant over time. However, in real-world scenarios, the system dynamics may change over time, posing challenges for model adaptation.

Despite these challenges, researchers have developed various extensions and enhancements to traditional HMMs to address specific limitations:

1. Continuous Observation Spaces: Traditional HMMs assume discrete observations, but many real-world applications involve continuous data streams. Gaussian Mixture Models (GMMs) or Gaussian Mixture Hidden Markov Models (GMM-HMMs) extend HMMs to handle continuous observation spaces by modeling the emission probabilities as Gaussian distributions.
2. Variable-Length Sequences: Standard HMMs operate on fixed-length sequences, but some applications require modeling variable-length sequences. Variable-length HMMs, also known as Variable-duration HMMs (VHMMs) or Variable-order HMMs (VOHMMs), allow for flexible modeling of sequences with varying lengths.
3. Structured Output HMMs: In tasks where the output space exhibits structured dependencies, such as sequence labeling or parsing, Structured Output HMMs (SOHMMs) extend traditional HMMs to model the joint distribution over both hidden states and structured outputs.

Conclusion

Hidden Markov Models have emerged as indispensable tools for modeling sequential data in a wide range of applications. From speech recognition to bioinformatics and beyond, HMMs offer a principled framework for capturing the underlying dynamics of complex systems. Despite their challenges, ongoing research continues to push the boundaries of HMMs, leading to innovative extensions and enhancements that further broaden their applicability. As the field of machine learning continues to evolve, Hidden Markov Models stand as timeless pillars, illuminating the path to understanding and modeling sequential phenomena.